已知曲线C:y=x2/2,D为直线y=-1/2上的动点,过D作C的两条切线,切点分别为A,B
(1)证明:直线AB过定点。
(2)若以E(0,5/2)为圆心的圆与直线AB相切,且切点为线段AB的中点,求该圆的方程。
解:
(1)做这种曲线题,图像肯定是灵魂所在,灵魂画手更是不可缺少的
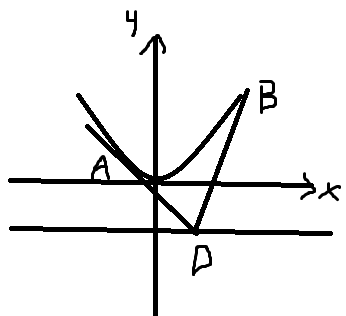
聪明的你一定发现了y=-1/2就是抛物线C的准线。
我们设A(x1,y1)B(x2,y2)D(t,-1/2),设直线DA的斜率为K1,直线DB的斜率为K2。
求直线AB过定点肯定要把AB这条直线求出来,那么既然用到了D点,那肯定说明A,B,D之间有某种关系。
直线DA:y-y1=K1(x-x1),直线DB:y-y2=K2(x-x2),尽量把未知数减少。
这里就用到了导数,因为y=x2/2,所以y'=x,即K1=x1,K2=x2
所以,直线DA:y-y1=x1(x-x1)直线DB:y-y2=x2(x-x2)
把D点带入直线DA可得:
-1/2-y1=x1(t-x1)
-1/2-y1=tx1-x12
继续把未知数减少,因为A在抛物线C上,所以满足y=x2/2,继续化简可得:
-1/2-y1=tx1-2y1,最后可以得到,tx1-y1+1/2=0,此时直线AD就算出来了。
直线BD不用算了,因为B点和A点唯一的区别就是坐标左下角一个是2一个是1,所以我们把直线AD里面的x1和y1换成x2和y2就行。
直线BD:tx2-y2+1/2=0
由此可见,A,B在同一条直线上。
不能理解?
比如现在有一条直线为:x+3y=0,A点满足x1+3y1=0,B点满足x2+3y2=0,这就说明A,B在直线x+3y=0上。
所以,A,B都在直线tx-y+1/2=0
定点就是(0,1/2) 刚刚好就是抛物线的焦点!!!
有部分同学不知道定点怎么求,接下来介绍2种方法:
①因为t不确定,所以直线是不断在变化的,要先求定点,首先就要把t去除,此时令x=0,所以y解出来就是1/2了。
②反正是过定点,那么t取什么这条直线都要过定点,我们取1和2,然后再把x-y+1/2=0和2x-y+1/2=0联立,也能求出定点(0,1/2)。
第一题其实还有一种更快的方法,不用点斜式去求直线AD和直线BD的方程,直接用斜率来求。
因为直线AD的斜率是x1,斜率又等于(y1-yD)/x1-xD),所以x1=(y1+1/2)/(x1-t),很快就求出x和y的关系了,剩下的步骤同上。
(2)老规矩,画图再说。
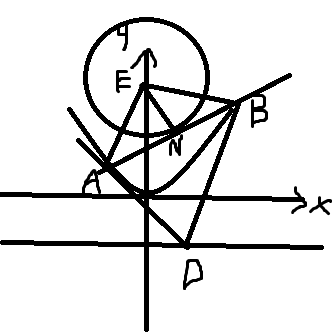
设切点为N,连接AE,BE,EN。N((x1+x2)/2,(y1+y2)/2)
看到x1+x2,马上想到韦达定理。我们把直线AB和抛物线联立,可得x2-2tx-1=0,此时△>0,x1+x2=2t,y1+y2=t(x1+x2)+1=2t²+1(由第一题可知tx-y+1/2=0)
题目似乎已经没有其他可用信息了,但是我们此时应该想到EN⊥AB
这个是题目的一个隐含条件。根据垂直能联立的式子有很多了,比如KENxKAB=-1,或者EM向量xAB向量等于0,甚至初中学的勾股定理,丨EN丨²+丨AN丨=丨AE丨²
这里我们就讲解KENxKAB=-1和者EM向量xAB向量等于0这两种方法。
方法一:
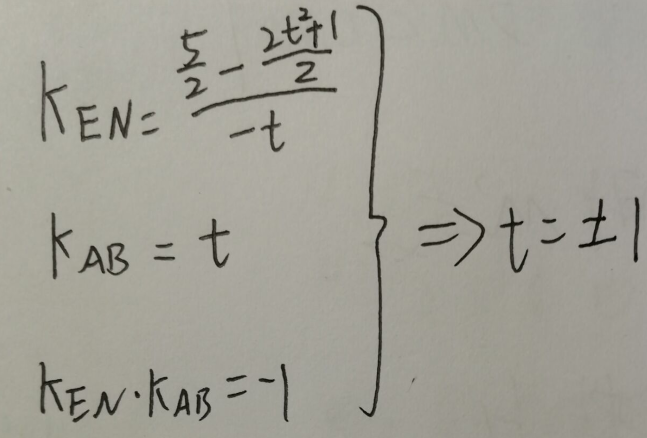
如图列式求解,可求出t=1或-1,所以t²+1/2=3/2,圆心为E(0,5/2),半径就是丨EN丨
求得丨EN丨=√2,所以圆的方程为:x²+(y-5/2)=2,你以为就这么结束了?大错特错!
KENxKAB=-1的使用条件是斜率存在,此时我们还需要考虑斜率不存在,如图所示:
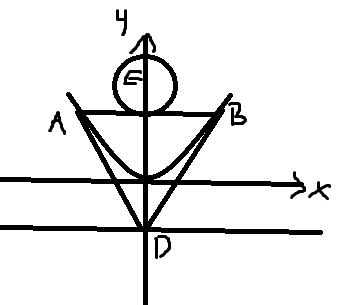
这种情况应该一眼就能看出圆的半径,这里就给个结果吧,x²+(y-5/2)²=4。
接下来,我们讲方法二:
N(t,t²+1/2),EN向量=(t,t²-2),AB向量与向量(1,a)平行,所以这里我们用(1,a)代替
解释一下为什么AB向量与向量(1,a)平行
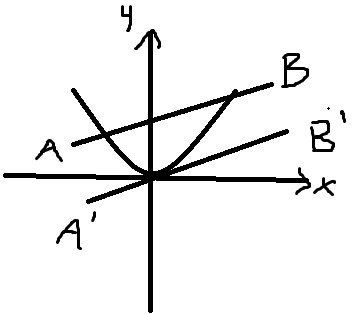
因为直线AB的斜率是t,因此直线A'B'的斜率也是t,设直线A'B':y=tx,取x=1(想取什么就取什么,想张扬个性可以取99999999999),此时y=t,令这个点为F如图

那么向量A'F=(1,t),AB∥A'B'∥A'F。
因为向量EN⊥向量AB,所以向量ENx向量AB=0,把向量AB替换成跟它平行的向量A'F,可以列出以下式子:
t+t(t²-2)=0,求得t=0或1或-1
当t=0时,向量EM=(0,-2),丨EM丨=2,所求圆的方程为x²+(y-5/2)²=4
当t=1或-1时,向量EM=(1,-1)或(-1,-1),丨EM丨=√2,所求圆的方程为x²+(y-5/2)²=2
PS:第一题和第二题都不止一种方法,按实际情况取舍,个人建议第二种方法,无需考虑斜率是否存在。
如果第二题实在想用勾股定理的话自个儿算去。


本文 暂无 评论